Arabic tattoos are definitively in fashion in the world of the rich and the famous. And I don’t mean temporary tattoos done with henna. This is perhaps surprising, because there are hardly any tattoos to be seen in the Arab World. In the West, however, tattoos have come a long way from the time when they were essentially associated with sailors and soldiers. Nowadays, having a permanent inking on your skin is no longer a sign of low class.
Recently, celebrities like actress Angelina Jolie, football player Zlatan Ibrahimović, and pop star Rihanna have been getting Arabic phrases and words tattooed on their bodies. But, do they really know the meaning of the words they are eternalizing on their skin? Let’s take a look at the tattoos and their meanings:
Angelina Jolie: the firm will
First off is Angelina Jolie who it seems has already filled every inch of her skin with some writing or other. Her latest addition is this Arabic tattoo:
Taking a closer look we can make out the Arabic word العزيمة (al-‘azeema), meaning “the determination” or “the firm will” on her right forearm. Jolie certainly strikes me as a woman who knows what she wants – so it seems that this tattoo is quite fitting. However, the word can also mean “the incantation” or “the spell”.
While the Arabic script chosen for the tattoo is pretty plain, Angelina (or one of her assistants) has at least done enough research to ensure that the word is spelled correctly – no slipups here.
Zlatan Ibrahimović
Moving on to Zlatan Ibrahimović, the top football player:
For those learning Arabic, the tattoo might be pretty confusing. Fear not, the solution is simple: the inscription is simply a transliteration of Ibrahimović’s surname – in Arabic إبراهيموفيج (ibraaheemoofeedj).
Since the Arabic letters don’t correspond one-to-one with our English letters, the tattooist (or someone who speaks fluent Arabic) had to choose something that is as close as possible to the actual pronunciation of the name Ibrahimović. For example, there is no “v” in the Arabic alphabet. The next best thing is the “f” sound.
Maybe the egocentricity demonstrated by Ibrahimović’s choice of word is not to everyone’s taste. But, at least the tattoo is spelled and written correctly.
Rihanna
Finally, let’s see what singer Rihanna has engraved on her waist:
The Arabic reads الحرية في مسيح (al-horriya fi maseeh), or in English “the freedom in Messiah”. Huh? Seems like Rihanna is quite a religious one, but why hide the message of salvation in Arabic rather than show it off to her (supposedly) bigger English-speaking audience? Perhaps her religious convictions are more of a private thing for her after all?
Well, be that as it may. What is certain, is that the phrase should have read correctly الحرية في المسيح (al-horriya fi al-maseeh), or “the freedom in the Messiah”. Not all is lost, though, since there still is ample space to insert the Arabic article AL before the word Messiah. So, Rihanna, another visit to the tattooist?
If you want to follow the celebrities’ example and get an Arabic tattoo yourself, then make sure that you know exactly the meaning of the words you are engraving for life. Better yet, why not learn the Arabic alphabet yourself so that you can be sure that the words are written correctly?
Watch out for my next post to be published soon on embarrassing errors to avoid when you are getting an Arabic tattoo.
Get over 1400 sizzling hot and accurate Arabic tattoo designs
If you’re looking for accurate and unique Arabic tattoo designs, then check out my new Arabic Tattoos collection.

Update: The second article about Arabic tattoos is up.
Update: If you want to see some good examples of tattoo templates, check out my two blog posts where I fulfill reader requests:





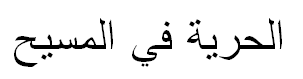




Hi i was wondering if you could send me a picture of “The Determination” in different fonts so i could take a proper look at it! I am thinking of getting this as a tattoo but i dont want to make any mistakes?!? Thanks very much xx
Hi Rachel!
You can find the picture containing “the determination” in different fonts in the comments section of my post here.
Enjoy!
Hi I wanted to get a tattoo in arabic script saying “BELOVED”……can you help me with that?
Hi Milena this is beloved in arabic just copy and paste it into wordpad and change the font to something bigger and you can have a good look at it الحبيب
Thanks for trying to help out Dean! However, I would like to point out that “beloved” has more than one translation. The one you gave – الحبيب – translates as “the beloved” and often has a religious meaning to it as a honorific title of the Prophet of Islam Muhammad. Other variations such as حبيبي (“my beloved/darling” for a man) and حبيبتي (“my beloved/darling” for a woman) might be better suited in some cases. If “beloved” is used as an adjective in conjunction with something else, it’s also possible to use محبوب (for a man) or محبوبة (for a woman).
Additionally, it’s not a good idea to simply copy and paste Arabic text if you aren’t familiar with the Arabic alphabet and have ensured that your PC can handle the Arabic script properly.
There are 6 designs each for the male and female version of “my darling” in my Arabic Tattoos eBook and 4 designs each for “beloved”. There are also designs included for “my beloved husband” and “my beloved wife” as well as 3 designs each for “beloved of my heart”.
Can anyone help with the translation for “Just Breath” as in to take a breath.
مجرد التنفس would this be correct and is any other ways that it could be understood?
So I wanted to just find the arabic translation and writing for “Free Spirited” or “hope.” Ive found a few translations for these but i wanted to make sure they are correct.
i want one that goes kind of similar to “posh’s”. the one that goes down her neck, but is it correct? someone contact me?
thanks.
ArabicGenie: I removed your e-mail address from this comment. Otherwise you might receive a lot of spam e-mails in the future.
MDR, are you referring to Victoria Beckham (“Posh Spice”)? I’ve taken a look at her tattoo that goes down the neck and to me it looks like Hebrew not Arabic. Or were you referring to someone else?
hi is there any way i could get the translation of NO STRUGGLE NO PROGRESS IN ARAB script
i’m looking into getting a Arabic tattoo. However, everyone is giving different versions of my tattoo. Please help I would like it to read….MY LIFE MY LOVES JOHN AMANDA WILLIAM
I’m thinking of getting an Arabic tattoo and would like it to say “Float through the chaos”
have tried some translation sites but when I have checked the results on other sites it hasn’t matched!! Which (if any) is right??? Help!!
تطفو من خلال الفوضى
فلت ثرغ ذي شوس
Hi, this is a brilliant site!
Can you help me with the translation of the question:
Will I know when I am living?
Many thanks!
can you help by translating Free as a Butterfly..
thanks
i was wondering if you could translate “Reach for the Sky” in Arabic. I want to get it as a tat.
thanks
hello, i really want to to get a tatto in Arabic, and i honestly do not want something spelled wrong on my body FOREVER. i’d love to be help , and have
” There is a light that never goes out”
– translated in a Arabic ; pleaseee ?, i’ll appreciate it with all my heart :o.
Hello Arabic Genie, one of my friends here in Mexico found this tattoo that she would like to get, but dooesn’t know the meaning. Could you please help? The text is أمي قلبي
Hi Rakesh! The Arabic text you provide is:
أمي قلبي
which translates as “my mother, my heart” or “my mother is my heart”, meaning that the speaker’s mother is very dear to him/her.
“there is a light that never goes out ; would this be it ? هناك ضوء أبدا أن يخرج
Hi there, I am looking to have “Grace” as in Grace of God tattoed in Arabic. I seem to have found a million variations. Grace of God seems easier to find and I wouldnt mind that if it is less likely to be the wrong context. Any help appreciated!
Thanks
Hi Christine! I recently did a blog post about “compassion” in Arabic. As it so happens, that same Arabic word I chose also means “grace”, as in grace of God. You can find the blog post with three designs for the word here. If you require more choice, better quality and a pronunciation guide, then please consider ordering a custom tattoo design.
meagain , I believe that translation is more an art than just a word by word transformation , in Arabic the term ” light goes out ” does not Exist i the exact wording , yet the translation comes from the understanding of what you want to translate .
Example ” there is a light that never goes out ” = ” there is a light that never Fade” = هنالك دائما ضوء لا يخبو ابدأً
note if this is a verse from a relegues script such as ” Quran, Bible,Tora” it is better that you take if from the Fully translated script itself ..
Yours
Abdulrahman
Hi~ I’m thinking about getting a tatto in Arabic. What would be the best way to say “Let there be freedom”? Thanks!
hey.. can anyone help me with my name in arabic letters for my tattoo?
“ANGELIN”
thanks !
hi there Angelin
since there is a kind of more vowel sounds in English than the Arabic you can write your name on both ways :
آنجلن
or
آنجلين
i go with the second one .good luck.
grace , you can say ” أعطني حريتي ”
which is more like ” let me free ”
but what makes it used a lot commonly that because of it’s a part of an old poem and a famous 60’s revolutionary song ,,
أعطني حـريّتي
أطلق يديّ
let me free
unlock my cuffs
hope you also considering the symbols above the letters cuz they are important some times with how the sounds are pronounced
🙂
Hi 🙂 , could you translate ‘passion, determination, love’ please? thank you!
kelly that would be “شغف,عزم,حب”
its all kinda sucks try to one its called امي نور عيني what it mean is momma the light for my eyes or try المجروح the meaning it like hurting or try الحب عذاب في قلوب الشباب
Hello! Love this site. I was just wondering if you can translate three words for me? It’s “belive” – not believe in god. (belive in myself) , the second word is “want” like (if i want something i can get it all I need is the willingness to try) and the last word is “dare” – If I have a wish or a will, I can manage it by daring to believe in myself.
I will tattoo those three words in my neck on my eighteenth birthday, those words means alot to me and i just love the arabic alphabet and words.
I would like a translation please faith, courage, strength
Hi Refiole!
You can find designs for all three of these words in my Arabic Tattoos eBook.
@Refiloe
إيمان، شجاعه، قوه 🙂
This is not quite right Mu7ha. The last two words should end in a taa’ marbooTa:
شجاعة
قوة
Also, it would be better to use the definite article al in front of the words, as we are talking about general concepts here.
Could you give me the phrase ” what comes around goes around” in arabic please? Thank you
I would like to get ” Love Kills Slowly” would this be the correct translation: يقتل الحب ببطء
Hello,
Can you please translate “Imperfection is beauty” in Arabic? One of my friends did it for me:
لعيب هو الجمال is that right? I just wanna be 110% sure it’s correct. I really want to get that phrase tattooed soon. I’d really appreciate it. Thank you!
Please help me translate “intermingling of souls”
Been trying to have it translated by my Hindu friends but they said the first word is complicated. Thank you.
Christine, I’ve answered your question in a new blog post here.
hi arabic genie i was just wondering if you could translate something for me in arabic. ‘yea though i walk through the valley of the shadow of death i will fear no evil for you are with me my rod and thy staff they comfort me’ if you could that would be great as i need it for a project im doin.
Hi Jay! I have fulfilled your request in a new blog post here. I’m curious, what is the project about?
Thank you. im doin an art project for college and im basing it on calligraphy and the bible.
also could you translate my mums name and my brothers. ’emmeley’. ‘Jordan’. thank you
Hi Arabic Genie,
I want to have my late brothers name and my daughters name in arabic tattoo’d in 2 seperate designs. My parents have translated for me but its been a while since they have used there mother language. The 2 names are Abigail and Samuel. Would really appreciate a seperate confirmation from you before I go to the artist.
Thanks in advance
Hi Simon!
The most common translation for “Abigail” would be:
أبيجيل
And for Samuel:
صامويل
Note, though that there are other alternative translations that are also in use for those two names. If you want me to create a tattoo design for the two names, please see this page here.
hi
would it be possible if you could translate my mum and brothers name please. ’emmeley’ and ‘jordan’. thanks
Helloo!
Does ‘life is not a rehearsal’ translate into Arabic or is there a similar phrase in Arabic wit the same meaning? Thank you!
Hi would you please translate my name ‘Kim’ please? Thanks
I think it would be interesting if you did a blog post about successful, correct Arabic tattoos to show people that if they are patient and research the accurate meaning/spelling of the words they will be extremely satisfied in the end. I have an Arabic tattoo that is 100% accurate which I absolutely love. When I see these pictures of these horribly executed tattoos, it makes me that much more thankful. If you were ever thinking of doing something like this and wanted to a picture of my tattoo, I would love to share it.
hi jay i’m syrian so i speak arabic very well and i can help u jorden is جوردن in arabic and emmeley is إيميلي as for kim it’s كيم and i’m sure 300% so if anybody has a question about translating just send me an email at ArabicGenie: E-mail address removed for your own protection. and i’ll be glad to help coz arabic is my native languege
how about this tattoo جمال الروح wich means the beauty of the soul
How about this tattoo إنت قوفمي إنت قولوم في هجتي …
it means Ente quavmi ente qulum fi hajati..is this tattoo spelled corectly?
thanks
Kristian, this text makes no sense whatsoever in Arabic. What is the original English text? You can hire me for a custom tattoo translation and design here.
It means: Your are my heart, you are everything in my life …thanks! 🙂
Ciao, vorrei che qualcuno mi traducesse “regina della mia vita” in arabo…….grazie mille!!! Spero in una riposta
i need mahmoud in arab writing for a tatoo
Hi Mike! Please refer to my custom tattoo translation and design service.
hello!could you translate this phrase for me please?
أنا مدمن على الحب
Alina, it means: “I am addicted to love”
Could you please translate
‘Neil’ and ‘Kylie’ for me please?
hello…i wanted to get a tattoo similar to rihanna, but i wanted freedon in God.Cant find the correct speeling different websites are giving me different things.Can you help me please.
Hello…I am planning to get my name in Arabic which is – ‘NUPUR’ ..can you please advice how my name would be written in Arabic..and also the zodiac ‘Leo’…!
Many Thanks
I’m an Arab.
I’m not into tattoos really, anyways, you are missing something here, you are trying so hard to translate English phrases to Arabic and most of times it doesn’t fit or show up in poor structure. Think the other way. Find someone who can provide with you phrases that are famous and well pharsed in Arabic culture and see the meaning in English.
For example:
مجنون ليلى
meaning” The one who’s crazy about Layla” /”Mad about Layla” very known romance character in Arabic history pretty much similar to Romeo the lover boy. Yeah and he’s a man so it wouldn’t fit 4 girls putting this one one. It best fit if your love is called Layla or Lila.
quick examples:
Peace be upon you السلام عليكم
ملكة سبأ Queen of Sheba
الحب الحقيقي Ture love
الأدهم name of a famous dark horse in Arabic literature.
الخيل والليل والبيداء تعرفني very famous poem starting line meaning “Horses, night and desert know me”
زرقاء اليمامة “Blue eyes of Yamama” a legendary woman in Arabic myth claimed to have the ability of seeing people as far as 3 days walking distance from her point of contact.
That’s it a toul alors! : )
If you want you can have my e-mail (it’s ok to share it websie Admin : ))and I’ll be happy to help.
Adel, welcome to my blog. I agree that often translations are somewhat awkward. This is especially true in the case of automatic machine translations such as those by google translate. Which is why it’s so important to have a real person do the translation. As for getting tattoos based on Arabic literature, poetry or folklore, I think it’s a great idea. However, it presupposes a solid understanding of Arab culture and will therefore only be an option for a few. In my book I have included a large number of tattoo designs that are based on expressions used in Arabic. Other expressions have been translated from English, but are readily understood in Arabic and don’t sound awkward.
hi could you please translate for me “life is too short to be scared” thank you
also i am looking for a good website with different fonts in arabic, do you know any professional ones? thanks
Hi Ela! I can certainly translate this phrase. Please go here and select “7 words” from the dropdown menu.
hi i was wondering if this is the proper way to write god is love in Arabic إله حالة حبّ
Hi Fae! Did you get this “translation” from a translation engine (e.g. google translate)? It certainly looks like it, because it’s wrong. The correct translation would be:
الله محبة
Please go to my custom tattoo design page to get high quality tattoo designs in Arabic for this phrase.
thank you
oh and another one how do you write and cause now i want to see how you write god is love and beauty of the soul
Fae, please refer to my custom tattoo design page.
Hi Arabic Genie….I wish I could have a reply to my query please??I want to know how can my name-‘Nupur’ be written in Arabic and also my Zodiac ‘Leo’…?Please advice soon…thanks again..!!!
Hey, i want to tattoo “love” in arabic. Is ” حب ” the correct translation?
I understand in arabic love can descirbe the love from a female to male and from a male to female but what is the simple word for “love” ? please help.
Nupur you’re name is written like this : نوبور
Jessenia, its better to write الحب
PS, Iam Arabic (:
Nupur, please go to my custom tattoo design and translation page for your name and provide pronunciation hints. For “Leo”, please see my Arabic Tattoos book that contains all the star signs.
Jessenia, الحب is correct. For six different designs of this word, please see my Arabic Tattoos ebook.
Hi. I have had various translations for the words ‘friend’ and ‘promise’. Can you please assist with providing a correct translation? Thank you in advance!!
hi, please i need this soon as possible, i would so appreciate if someone emailed me how to properly write this in arabic, i don’t mean a word for word translation, but the correct way to put this sentence in arabic, “our stones can break their bullets” to my email: ArabicGenie: E-mail removed to protect you against spam
thank you so much
Omar, if it’s urgent, then you should consider my custom tattoo design and translation service.
HI
I WOULD LIKE “TO LOVE IS TO LIVE” WRITTEN VERTICALLY DOWN MY SPINE AND HAVENT BEEN ABLE TO FIND A TRANSLATION. PLEASE HELP X
Can you please post on here how “Sagittarius” and “Penny” are written in Arabic? I can’t seem to find it anywhere!!!
Thanks for your help!
could u translate ” Whoever knows the meaning of life figured it out after they died or after they spent the evening with christ”
can you translate “don’t dwell?”
Hi could you translate “my parents are my heart” into arabic please. or if you know a phrase that sounds better? i want to get this on my wrist, so dont want it to be to long. Also what is Leyla in arabic?
Hello! This site is amazing! I am wanting to get innocence is beautiful tattooed onto me but the translation engines I found didn’t match up. I visit egypt every year and would be mortified if I got something that wasn’t a correct translation. Thank you so much.
Hello!
I wonder if you can help me…… I would like the following names in arabic but to read down my spine. How can this be done??
Graham
Karon
Leigh
Simon
Thank you
heyy, i want to get a tattoo in arabic that says “walk without fear” , what is the translation for that in arabic? please help me 🙂 it would mean alot, thankss.
hey victoria ,, it’s
أمشي بلا خوف
=)
Victoria, please see my Arabic Tattoo Design service for custom translations and designs.
Louise, to get vertical writing you will need to rotate the Arabic writing by 90° counter-clockwise. This way the connectedness of the letters is preserved. Most Arabic letters are connected to each other, regardless of whether they are written by hand or in print. This is why it would be uncharacteristic to write the letters separately from each other one above the other…
i need somebody to translate “family is a heaven in a heartless world”
Hello! Could you please translate the names Fatima and Nowreen and the words Mother and Sisters for me? Or better yet, I want a tattoo of a phrase that shows my love for my mother and sisters. Could you provide me with a beautiful and poetic phrase in arabic that suits that? Your help is greatly appreciated, thank you!
Hi from Montenegro,
Please 2 names in arabic ELDISA ELDIN
Thx
Hi, Can someone please tell me how to write the following:
“I Am Me” and “Be”
Hello Arabic genie, would u pleeze translate ‘queen of Sheba’ into Arabic text for me? I know it’s ‘malika saba’ but I don’t know how to write it in Arabic. Thanks.
Please refer to my Arabic tattoo design service.
Arabic Genie: How do I say Never Give Up in Arabic?? How is it written.
to Dfras
لا تستسلم أبداً
Dfras, I discuss the different translations for “Never give up” in this post here.
can anyone tell me what this phrase would translate to in english?
على العالم قد تكون شخص واحد فقط ، ولكن بالنسبة لي كنت في العالم.
thank you!!
CAN SOMEONE TELL ME HOW TO TRANSLATE “SINS OF THE FLESH” IN ARABIC PLEASE.
Sara, not quite sure if that sentence makes a lot of sense. Literally it says: “On the world you are maybe only one person, but for me you were in the world.” The second part could also read “but for me I was in the world”. In either case this sounds quite strange. Is it something you translated yourself into Arabic?
Estella, please don’t write in all caps here. Regarding your question, please refer to my Arabic Tattoo design service. Thanks.
Great website..I am not sure how i go about this but i have been looking for a nice design for my tattoo..it is to say “abu nadim” in arabic..feedback is appreciated..
@baj.na: Please head over to the custom tattoo design section and select “two words” from the dropdown menu. Current turnaround time is two working days. Thanks.
hi what would ‘Only God Can Save Me’ in arabic???
@ Stephan
Only God Can Save me = الله هو الوحيد الذي يستطيع إنقاذي
Please can someone be soo kind and help me 🙂 i would like to get a new tattoo in arabic saying “dream as if you live forever, live as if you die today” this is what ive come up with الحلم كما لو كنت تعيش إلى الأبد يعيشون كما لو كنت تموت اليوم does this make sense? please help.
also live يعيش
laugh ضحك
love الحب
are they correct?
please rite back on here or e-mail me E-Mail Removed Thank you x
ArabicGenie: E-Mail Removed for privacy reasons.
Mel, the translations are completely wrong. Did you use Google Translate? I can certainly help you with a proper translation. Please see my custom tattoo design service.
Could someone translate ‘what does not kill me makes me stronger’ into arabic text for me please
hey sara, the translation is:
ما لا يقتلني يزيد من قوتي
i could any one translate this into arabic for me please. “Dont Dream It Live It”
Sarah, this translation is not completely wrong, but it’s certainly not elegant. For a proper translation and tattoo design for “what doesn’t kill me makes me stronger” you should take a look at my custom tattoo design service.
for sara
on sep 6 2010
على العالم قد تكون شخص واحد فقط ، ولكن بالنسبة لي كنت في العالم.
for the world you may mean just a person, but for me you mean the whole world
any quastion e mail me at
ArabicGenie: E-Mail removed for privacy reasons.
for sarah oct 8th 2010
ما لا يقتلني يزيدني قوة
the translate is soo correct and u can change the style of writing, there are so beautiful writing style that is good to be a tatto i have made one to my best friend. it said ( live your life ) in arabic just let me know!!!!
ArabicGenie: E-Mail removed for privacy reasons.
@Moe: Your translation of Sara’s Arabic phrase (Sep 6 2010) is certainly incorrect. In fact, as I explained above, the Arabic doesn’t make much sense and is grammtically incorrect!
Hello.. I was wondering if someone could translate my fathers name in to Arabic? I am hoping to have the text as a tattoo. His name is ‘celal’, and I think it can be spelt jelal as celal is the turkish spelling. Thanks 🙂
how do write Brian in arabic? please help me..write me back..thank you
I love this kind of tattoo, It’s really interesting to see tattoo which you do now understand.
I really hope to have it.
@Anna Amaya… You can use Google Translate for your name translation.
by
Rey, I would strongly discourage anyone from using Google Translate for tattoo translations in any language. The results are often disastrous. Much better to engage a human translator.
hi arabic genie i was just wondering if you could translate my mum and brothers name would be truly grateful. ‘Emmeley’ and ‘Jordan’
thanxs
I wan to know how to say “twins” in arabic…can you help me please?
Sir –
Need your help please…can you please translate, “Have faith” for me?
Thank you very much!!
Hi! I was wondering if this is correct for “You Live and You Learn.”
أنت تعيش أنت تعلم
hi what would “independence” be in arabic? is the google translations correct?
thanks-
Hi.
I m new to Arabic tattoos. Living in a country with biggest moslem population, Indonesia, I found out Arabic writing is very beautiful. Could someone please help me with translation of “I am Remarkable” ? Otherwise, I will have the Rihanna’s arabic tattoo soon.
Thank u so much
Hi
I want to get F***in Perfect as a tattoo, it’s a song by P!nk and its my favorite song. I am arabic and I’ve been asking my parents to translate different things but they didn’t know how to translate this. I found it online as فوكين الكمال but I wasn’t sure if it was right. Can you help me out?
hello can you translate,,
live love laugh
thank you very very much!
Could someone translate into abaric or latin “friendship, love and passion”?
Jare, friendship – الصداقة – love -الحب – passion – الشغف – , all in arabic.
Hi,
I’m getting a tattoo in a few days and i would like it to say ‘My Beautiful Rochelle’ i have tried many translation sites but they all say different, Please could you tell me the correct translation, i think Rochelle is
روشيل
Hi
I’m trying to get “Imperfection is Beauty” as a tattoo in Arabic.
Any help with this?
hey!
Can someone please tell me what friendship, love and passion are in Arabic? Or even what they mean by symbols’?
I would really appreciate
huhuuuu
Im A-Extreme
hey I need to know the translation of–” for the strength And love of my brother Adam” Its a tattoo. I have to have..I appreciate it much.
hw=ey can you translate ‘to be wise you must first be young and stupid’
a tattoo i want.
thanks
Hello there, I was wondering how to translate “Boston” and “What is the point of confessing if you don’t repent” into Arabic please :-)x
hi i been thinking of getting a tattoo
one with the word love and one withe the word believe (as in believe in love)
i was wondering if i had it right before getting it for sure.
love الحب
faith/believe الايمـان
thanks for your help 🙂
Hi Erica! Please see this blog post here for “believe” in Arabic and that one here for “love” in Arabic.
I want to get “anthony” tattooed on me in arabic but I’m not sure how to do it. Can you help me?
i am wanting a new tattoo in arabic writing i have been checkin google translate but it dont look write could you please write for me correct way
Live life to how you want dont let others live it for you
Live life regret nothink
hey i need the translation of mummy in arabic as my mum not long passed would like this tattooed..great if anyone could help!x
Hi can I please have the translation for two names 1) Kayleigh. 2) Ciarra. And also the phrase – my love for my family knows no boundaries. – daddy’s angel – may god protect you. I have tried to write these out but my Arabic is very rusty as I have lived in the uk for 15 years now and forgotten the grammar, thanks for the help guys.
hi arabic genie. i really want an arabic tattoo and would like you to translate “she will be loved”
Hello Arabic Genie, I was wondering if you could translate “magical” into Arabic for me? Using it as someone who has powers or has a liking for magic. Also, if not too much, could you translate “hero” as well? It would be greatly appreciated. Thanks a lot. (:
I want to get a tattoo that says “God is the strength of my heart” is this the correct translation? الله هو القوة من قلبي
And If I wanted to break it up into either 2 or 3 lines how would it be written??
Also anyone have ideas on what I can put this phrase in or a drawing by it???
Thank you!!!!
your phrase mean :”god is the strength from my heart”
الحرية في المسيح
Means “Freedom in Christ”
I want to get a tattoo in arabic. What is the best way to have Learn from yesterday, live for today, hope for tomorrow? thank you.
Hey, how do you translate “Only god can judge me” ? thank you.
Hello. i’m going to have my first tattoo on friday, but i still don’t know what to write. been looking for the short proverbs, and i want my tattoo to be in Mashq or Tuluth style. any suggestions you can give me? is it lame to write my name as a tattoo? how can i get your book in Indonesia? Thanks before, and great blog! 🙂
Fist of all, LOVE THIS BLOG!!!!
Im looking forward on getting my fist tattoo next month, and since its going to be something thats gonna be with me my whole life I want it to be perfetc.
What I want to het is: JUST THE FIVE OF US, but it arabic. I have tried alot of translation sites but all of them give me something diferent.
Can someone please help me??
hi id like to get a tattoo saying ‘ i think about more than i forget’
ive looked on google translator and various other websites and they all came out similar أعتقد أن أكثر من حوالي أنسى can anyone inform me if this is incorrect a.s.a.p
i think about more than i forget’ = افكر اكثر من اني انسى
Hey there, this site is fantastic!
What is “When will I know when I am living?” in arabic?
Any help with this would be much apppreciated!
Many thanks,
Romeny.
Im looking forward on getting my fist tattoo next month, and since its going to be something thats gonna be with me my whole life I want it to be perfect.
What I want to het is: JUST THE FIVE OF US, but it arabic. I have tried alot of translation sites but all of them give me something diferent:
فقط في خمس من الولايات المتحدة
فقط خمسة منا
Can someone help me? I would like to know which one is the correct one!
Can someone please help me??
hi can i get strength, believe, you are strong and do not cry get even translated into arabic?
thanks
Are these correct?
do not cry get even لا تبكي حتى الحصول على
believe نعتقد
strength قوة
you are strong كنت قوية
hello,
i was hoping you could translate “impossible is nothing” for me? thank you.
Hi,
I’d like to hire you to make me a personal Arabic tattoo design but before I do so, I want to check a few things. Do you make different designs on the computer or do you write them yourself? I’d like to have my daughter’s name Zara tattooed on my wrist and I know how to spell it (زهرة, flower Zahrah) but am too scared to make a stencil myself and am not happy with this computer version. I have also had some native speakers write it for me + I’ve had it engraved on a ring in Tunisia, I still haven’t found a version that would fit on my wrist but isn’t too simple, eg. my Iraqi friend has given me this really ornate version that wouldn’t work on my wrist as it’s too detailed whereas some other simpler versions are not precise enough. Anyways, how do you do it? Thanks a lot
Can someone translate “I am me”?
hello 🙂
just wanted to know how you write ‘seize the day’ in arabic. and also how you’d write the word ‘fate’. thankssss a lot :)!
Hi Carol. There are three different tattoo designs for “seize the day” and six different designs for “destiny” in the Arabic Tattoos eBook.
hello,
i was wondering if you could give me a translation for ‘ wake your dreams ‘.
Online translaters give you dodgy font also so i was wondering if you could find a nice one for me, i can’t find a way of putting the two together.
Please and thankyou x.
hi, is this إن شاء الله, the correct way of writing Inshallah?
Hi ArabicGenie do you know the translation for “That that does not kill me makes me stronger” i have done various searches but keep getting different results…??? is there a phrase in arabic that means the same……???
Hello, please help me translate ‘never stop dreaming’ into Arabic please! I would really appreciate it if you could 🙂 bobbie x
to Bobbie , i cant actually translate ur sentence literally cz that way ur tattoo wont have a meaning in arabic ! but i suggest u this sentence in arabic لا تجعل أحلامك تتوقف
to Chris
in arabic we have a similar proverb wich means the same it’s
الضربة اللتي لا تقتلك تقويك
to Jade
the right translation is أيقظ أحلامك
CAN SOMEONE TELL ME HOW TRANSLATE “Im Nelča” IN ARABIC PLEASE. :o)
Hey, can you tell me how it’s spelled, “Susana Emmanuel”
This is truly awful. Hundreds of people want to get a tattoo in a language they can’t even read, or understand. Embarrassing. Why not just go with your native language? A serious question!
@Sara: As long as people make sure to get the correct translation for their Arabic tattoo I think it’s perfectly acceptable.
Hi,I want to get a tattoo in Arabic that says “One who stands out from the rest”.What’s the correct script?
Hi i’m really wanting to get the moroccan proverb “he who has nothing to die for has nothing to live for” tattooed i would really appreciate it if someone could help me out thanks!
Hi, im looking for a translation for ‘praise no one’ into arabic for a tattoo. can someone help me with this? thanks! x
“This is truly awful. Hundreds of people want to get a tattoo in a language they can’t even read, or understand. Embarrassing. Why not just go with your native language? A serious question!”,, I totally agree.
Okay when chinese words were the hit we understood but now people actually say bad stuff about arabs; they hate their lives, their religions, and so on.
The most fashionable tattoos worn by rich and famous people are in arabic. How come? LOL that’s so sad.. Don’t you people have your own language? Aren’t you proud of your native language? HAHA!
Hi, I want to get the quote ‘this is our fate’ its a quote from my dad and my favourite song – i also want to get it translated into arabic because I’m half. How would thi correctly translate please?
In arabic
Susana Emmanue سوسانا ايمانويل
my mum امي
never stop dreaming لا تتوقف ابدا عن الحلم
the destiny القدر
he who has nothing to die for has nothing to live for من لايملك شيء ليموت لاجله ليس لديه ليعيش لاجله
this is our fate هذا هو مصيرنا
wake your dream ايقظ احلامك
My Beautiful Rochelle’ جميلتي روشيل
“impossible is nothing لاشيء مستحيل
anthony انثوني
life is too short to be scared الحياة قصيرة جدا لتكون خائفا
he who has nothing to die for has nothing to live for sorryyy من لايملك شيء ليموت له لايملك شيء ليعيش له
magical سحري
Only god can judge me الرب فقط يستطيع الحكم علي
‘to be wise you must first be young and stupid’ لتكون حكيما يجب اولا ان تكون شابآ وغبيآ
Imperfection is Beauty العيب هو الجمال
queen of Sheba ملكة سبأ
family is a heaven in a heartless world الأسرة هي الجنة في عالم بلا قلب
what about ” what nutures me detroys me”
and ” my sisters keeper” please.
can anyone help me how to write mapata in arabic? plz reply soon
Gostaria de saber como se escreve “liberdade” em árabe.. sendo qe na vertical.. como se tivesse escrevendo de cima pra baixo!
ashutosh..
what’s this mapata.. ? i guess it’s a name.. anyway it can be written in arabic this way مباتا
Amanda
liberdade can be translated into حرية
hello, i would like for these to be translated please!
“victory favors those who take pain”
“there’s always tomorrow”
“walk by faith, not sight”
“with god nothing shall be impossible”
“It’s the end that counts”
thanks soooooo much !
I’m having trouble translating my son and my name in Arabic can someone please help it will mean alot to me! SON NAME:ANEURYS ME:SCARLET thnks!
PS:great blog!
I got my first tattoo 2 days ago. it’s the arabic word المسافر (if you don’t know Arabic, you read it as al-musàfir) meaning the traveler, or the wanderer. I LOVE IT! (:
greetings from Italy
Hi there,
I am about to get divorced for the second time and I want to get something meaningful tattooed onto my wrist. I cannot seem to find a proper site that will translate what I am looking for correctly. Please can you translate the following for me.
“I alone”
“Never Broken”
“Freedom” or “independence”
Would really appreciate it
please can you translate this in to arabic for me as i would like it as a tattoo love pleasure and desire
thank you would be very helpfull
Freedom الحرية
independence الاستقلالية
I alone انا وحدي
some expressions such as “never broken ” cannot be translated in to arabic but you can say
i’ll never break لن اتحطم ابدا
love pleasure and desire الحب المتعة و الرغبة
scarlet سكارليت
may someone who speaks the arabic language, please translate the following:
“Sagitarius”
“Believe”
hi taylor you mean Sagittarius ?
Sagittarius القوس
Believe صدق
Believe me صدقني
iam casar boy iwish yor see
Hi I am sorry to be a pain as I can see you have a lot of people asking for your help but i was wondering if you could please translate “you are my sunshine” for me.this is what I have at the moment but I’m not sure if it is correct, your help would be greatly appreciated. كنت لي الشمس المشرقة
Hi can you please translate my daughter Chyanne and son Baby Boy. Thank you
Hello everybody..
@katie… “YOU’RE MY SUNSHINE” what you got is not right..
the right one is ” أنت ضوء شمسي”
this is definitely the right one.. i’m an arabic guy..
and i can tell you that all online translators get helpless when it comes to translate a sentence..
Hi sir.
i was wondering since sarah was originally named sarai in the bible before she changed it wouldnt the two names be the same?
and if so, can you translate “women of high rank” in arabic.
cause i want to get that tattoo’d on my foot cause my name is Sarai.
than you so much 🙂
I don’t actually know if they would be the same name but the translation is
نساء المراتب العالية
Hi, I was wondering if someone could check this translation for me:
“All of our dreams can come true, if we have the courage to pursue them.” -Walt Disney
يمكن لجميع أحلامنا تتحقق ، إذا كانت لدينا الشجاعة لمتابعتها.
& “Mistakes are the portals of discovery” -James Joyce
الأخطاء هي مداخل الاكتشاف
Hi, i just wanna know if this is the correct spelling:
باسم الأب والابن والروح القدس، آمين.
[bi esm l ab wal eben warou7 l kodos. amin.]
(in the name of the father, the son and the holy spirit. amen.)
Hello!
I need help translating, any help would be greatly appreciated!
I’m looking to get ‘Liberate my soul’ tattooed in Arabic.
Can anyone tell me if this is the proper way to say that, or if there is a similar saying in Arabic better suited?
تحرير نفسي
Thanks in advance! 🙂
Hello..
@bailey the first one should be يمكن لجميع احلامنا ان تتحقق, اذا كانت لدينا الشجاعة لملاحقتها
the second one is good
@Patrick Abde.. you got it right.
@TattoGirl you… it is the proper way to say that.
itmeans that RIHANNA loves jesus “الحرية في المسيح” = freedome in jesus 😀 😀 <3 jesus
HELLO can you send me a picture of the words only God can protect me in Arabic? possibly in different fonts? THANK YOU!
“Only God can protect me”
THANKS!
Hi I please can you translate “Nana & Grandad” to Arabic I can’t find any where 🙁
hi can you translate this. samsean,vergo
hahaha
A lot of the word are JUST wrong !! And this come from arabic women (( thats me 🙂 ))
Not anyone can translate english to arabic
You must have arabic pirson to translate to you cous arabic is so hard to traslate
Hi how are you my name is jorge I was interested in getting a tatto in arabic letters but I don’t kno how to write it in arabic what I want to get tatted is — IN GOD I TRUST— can you please help me and thank you
Hi I am looking to get my daughters name (Grace) tattooed in arabic but have been given four different version. can you tell me if either one is right and if not what is it please?
1 . كريس
2 غرَيس
3 جريس
4. غرايس
Hi I’ve been wanting an arabic tattoo saying God is love but I still can’t find the correct spelling and I don’t want to get what google translate says ill be walking around with something thats not what I wanted. Please help me..
Hi Arabic Genie, Can you let me know what is correct or close to arabic translation for this english phrase.. ONLY GOD WILL JUDGE ME. i tried to use the goggle translator and this is what i got. ” إلا إرادة الله القاضي لي ” is this close/near translation?
Pls. let me know i want this as my very first tatoo.
Hi!This is a wonderful site!could you please write how would be these names in Arabic!
VELGA and the second PATRIC?Thank you very much!!
Can anyone translate the James Dean quote “dream as if you’ll love forever; live as if you’ll die today” into Arabic as I would like to get this as a tatoo but the google translators are wrong.. Please help 🙂 thanks x
To whomever wrote the article. Rihanna is not religious, in fact she is anti-religious. She is referring to al-maseeh ad-dajjaal who will set her free. She will add the Al when he appears. So I agree with you on this one, she will need another visit to the tattoo shop.
PS Google Rihanna subliminal messages
Omar
Apologies if I missed it but does anyone know what Hashish is in arabic?
Hi!! Could you translate the following for me in Arabic “He who dwells in the secret place of the Most High shall abide under the shadow of the Almighty. I will say of the Lord, “He is my refuge and my fortress; My God, in him I will trust. He shall cover you with his feathers, and under His wings you shall take refuge”
Its a few verses from Psalm 91
if you would like a second opinion on arabic tattoo translation, hit me up
and to john: hashish originally means GRASS, but it is also street languange for marijuana in most arabic countries…
Hello
I wanted to ask if you could translate
My kids name in Arabic I would need to get it design by you but I would like to know how they would look, and also are you a native speaker how many years how you been doing this is my first tattoo so I wouldnt want anything missed spelled ..
Jose
Josue
Jasmin
David
Thank you so much
Hello I was wondering if you could translate “love” for me
@Duraid Dalli – Apologies I know what it means I was after it in arabic, I’ll give it a couple of days and if I dont hear off you on here I’ll email you, thanks.
I hate when celebrities jump on ethnic heritages like it’s the latest craze. And for those of you wanting Arabic tattoos, I know I might get a lot of hate for this, but unless you are familiar with the culture, the language, or it means something to you to personally to have something done in Arabic, please don’t get it. It’s not some pretty cursive, it is a language with an ancient history, customs, and represents a large ethnic population and an even larger religious population. And please refrain from religion based tattoos in Arabic. I’m pretty sure the Bible, and definitely the Quran, frown on such things, so I would NEVER get anything like “Allah” (swt) or “Prophet” or anything even remotely similar to that.
Hi would Leo the name be the same as in the zodiac symbol..
Many thx
Can someone help translate me the following : ” I see my mother’s smile, that’s a blessing. ” I’d like to get it tattooed and must be sure that I have the correct translation in arabic .
@Maggie – first i just want to know if you are speaking Spanish or Portuguese or English cause it’ll make such different in the pronounce of your children’s names in Arabic .. it’ll be like that .. ” جوزيه – ياسمين – دافيد ”
@Rosa – love means in Arabic ” حب ”
@John -do you ask about what hashish mean in Arabic ?
@ricky barolo – you asked about the translation of ” ONLY GOD WILL JUDGE ME ” to Arabic .. so its translation is ” الله فقط من سيحاسبني ” or ” الله فقط من سيحاكمني ”
@Velga – the names in Arabic it will be like that
فيلجا – باتريك
@marite – the translation you asked about is ” الله هو الحب ”
@Donna – the translation of James dean quote to Arabic is .. ” أحلم كما شئت كإنك ستحب للأبد ، و عش كإنك ستموت غدا ”
@Archy – the translation you asked about is .. ” إني أرى إبتسامة أمي ، و هذة نعمة “
hello can someone please translate me the followin…
Never a failure always a lesson
i would also love if u can help me out with the following names…
ivette jacob miguel
please if i can get the arabic translation
@klaudia – the names in Arabic are .. ميجيل – يعقوب – إيڤيت
@ Ahmed
omg thank u sooo much..
i appreciate it..
do u know the translation to
“never a failure always a lesson”
has anyone bought the book? i want to buy it cause i want to see all the different types of translations.. but i dont want to regret buying it…
@klaudia – always welcome 🙂
yes i know the translation .. but i think that this sentence isn’t complete cause i think there’s something missing .. or it’s just like the tattoo on rihanna 😀
anyway in Arabic it means ..
كل خطأ ليس فشل و لكنه درس دائما
and it could be written in other way 🙂
@ Ahmed
thanks…
i didnt know rihanna has that but i love the quote…
once again thanks..
@amed
does this mean ivette
إيفيت
thats my daughters name.. but with an “I” not a “Y”
i just want to make sure the one u gave me is with an i not a y
thanks
what does this say?
ميغيل
@klaudia – yes ivette means إيڤيت .. it’s the same in arabic if it is with an ” i ” or ” y ”
but there’s a small note about it , that if you put the name ” ivette ” in google translate it will be ” إيفيت ” like what in previous comment .. but the right one is what i wrote ” إيڤيت ” because above the middle letter suppose to be three dots .. not one dot .. cause one dot pronounce like ” F ” but three dots pronounce ” V ” in ivette
I think you understand what i mean 🙂
and the second name which is miguel is written in arabic in both ways
ميجيل
or
ميغيل
Hi can you still offer a custom translation for a name?? I would really like to have the wording written in calligraphy, I am Lebanese but have lost touch with reading and writing Arabic and really want to have my daughter and wifes name tattoo’ed on me.
I am looking to translate the following.
Kayleigh (wife)
Ciarra ( daughter) or Cece ( nickname)
And maybe Safadi / al Safadi (my surname)
Thank you very much for your help
Phil Safadi
Thought I should point out that my daughters name is pronounced C-A-RA or similar to the pronounciation of car in Arabic, many thanks.
thanks ahmed!
How bout this quote?
LOVE HURTS,
LOVE IS EQUAL,
LOVE IS FREEDOM,
LOVE IS HUMAN EXPERIENCE, NOT A POTICAL STATEMENT.
@ahmed
thanks thanks thanks 🙂
ur the best lol
i appreciate u taking ur time too reply back….
hello can you translate me in arabic the phrase “where is your star ? “
@Safadi – your wife’s name in Arabic is ” كايلي ”
and your daughter’s name is ” سيارا ” and her nickname is ” سي سي ”
and your name is ” سافادي ” and your surname ” السافادي ”
you are always welcome 🙂
@ricky barolo – the quotes you asked about are in Arabic ..
LOVE HURTS .. الحب مؤلم
LOVE IS EQUAL .. الحب مساواة
LOVE IS FREEDOM .. الحب حرية
about the fourth quote .. there’s a little mistake in the word ” POTICAL ” what you exactly mean ?
@klaudia – you’re welcome any time .. and if you need anything again , I’ll be pleased to help you 🙂
@penelope -hello .. the translation to Arabic is ..
1- if it’s to a woman it’ll be ” أين نجمتك ”
2- if it’s to a man it’ll be ” أين نجمك ”
🙂
How would I write ” protected by Allah” in arabic
And ” freedom”
@humi freedom is الحرّية in arabic. some people might spell it الحرية as well. the difference is in the the little character above the Ruh letter. it’s called Shadda and is used to stress on a letter. it’s pronounced Al-Horriyuh. please note that the use of ال at the beginning is optional because it’s an article. meaning, you can use حرّية alone 🙂
as for protected by Allah, you can use تحت حماية الله (which is accurately the translation of “under the protection of Allah” or “under Allah/God’s protection” but they all mean the same thing)
I’m Lebanese, trusted source 😉
t: @ghostofyouu
f: facebook.com/joelle.evergreen
@Ahmed – I know what hashish means I need the word in Arabic, thanks.
@john – u meeean hashesh >> weed ! or wat if u mean it ! it like that in arabic ( حشيش )
if anyone wannt to help ,, i’m here !
@John – hashish in arabic is حشيش
How do you say no pain lasts forever in arabic
@ Ahmed hii its me klaudia again lol
can u help me out with this name?
فرانسيسكو
can u tell me the name??
kloudia
فرانسيسكو = Francisco
Crystal
it means in arabic = لا ألم يدوم إلى الأبد
Hi everyone! I would really appreciate it if someone could help me out with a couple translations. Please & thank you! 🙂
1. Intelligence is ignorance
2. Beautiful soul
I woul like to get a tattle of my 7 month old sons name in Arabic. His name is “Leo James” or maybe would be nude to have ” my little lion Leo James”
Oops tattoo I mean
hello, i want a tattoo in arabic saya i love my mum
:):) <3
hi could you translate this quote into arabic please..
“The greatest adventure is what lies ahead.
Today and tomorrow are yet to be said.
The chances, the changes are all yours to make.
The mold of your is life is in your hands to break”
and also this phrase..”I see my mother’s smile, that’s a blessing” thank you
Hi im really wanna get a tattoo done in arabic saying..life won’t wait..
will it make sense in arabic? iv tried to translate on google but im not sure its right..please help!
Can you help me write my name Giuliana in tuluth?
Hi,
Can you please translate “somewhere over the rainbow” into Arabic for me?
Thank you
I just posted but forgot to add that this is what I have. Is it correct? في مكان ما فوق قوس قزح
How about this tattoo إنت قوفمي إنت قولوم في هجتي …
it means Ente quavmi ente qulum fi hajati..is this tattoo spelled corectly?
thanks
………………………………………………………….
I am an Arab
And this sentence does not mean anything wrong
إنت قوفمي إنت قولوم في هجتي …
في مكان ما فوق قوس قزح
Does this mean “somewhere over the rainbow”? Someone please help!
Thank you!
Could someone help me and traduce : LOVE AND HAPPINESS in arabic?Thanks
to malia: u r right, somewhere over the rainbow means
في مكان ما فوق قوس قزح
to isabella: LOVE AND HAPPINESS means
حب و سعادة
dear fofo
this sentence does not have any Arabic meaning at all
How to write beautiful strong soul, sadaf (name) and Love in arabic
Hi Arabic genie could you translate everything happens for a reason into Arabic please? I have google translates it and taken it to Egypt but basically he one I got said it but in a different way could you clarify what you would translate it to please. I’m getting it on my ribs and wa wondering does it matter which side I get it on as Arabic is read from back to front but I also tho mall tattoos should face forward. Sorry for he long message could you let me no ASAP as I say have it booked for Saturday thanks Rebecca
Can someone tell me how translate “FARIZ” in arabic please…
Hi there, would love a translation of a date please if possible December 29 2011….my sons bday!
Sorry I know you have a lot of people asking for translations!
I just wanted to get the translation for Stuart I think its this: ستيوارت
Thank you very much.
I am looking for “true colours” in Arabic I know it doesn’t translate well but still would like too see it written
Can anybody help me what this tattoo mean?
http://weheartit.com/entry/30815778
That’s not Arabic…
How.to write beautiful soul in arabic.?
@ Sadaf: روح حلوة or روح جميلة
Hi there, could you help me translate the word ASIA into arabic?
THank you so much
You are my Sunshine (Male) = انت شمسي المشرقة
You are my Sunshine (Female) = انتي شمسي المشرقة
hello every one…can help me pls to translate this phrase in to arabic plsss: MY FATHER GAVE ME WINGS AND MY MOTHER TEACH ME HOW TO FLY thank you very much…it will be very helpful 4 me..thx again.
Hello,
Can you help me with the two below translations in Arabic:
1. Dream as if you live forever.
2. Trust is beauty.
Can you please translate “Without Struggle there is no progress” I googled it but I’m not sure if it is correct
I disagree with your statement “… there are hardly any tattoos to be seen in the Arab World.”
My grandmother is from Algeria and has tattoos on her face and on both her arms (full sleeves). Granted Algeria is in North Africa and we have more tribal influence, but similar tattoos exist in Libya, Jordan, and a few other countries.
Also, one quick type correction, Rihanna’s tattoo is on her waist, not waste. Thank you for a very informative article!
Laila, thanks for your comment. I guess I was remarking generally on the fact that tattoos are not as widespread in the Arabic speaking world as in the West. However, you are right, of course, that tattoos have been a traditional custom in a number of countries, such as Algeria or Iraq. Very interesting to hear about your grandmother’s tattoos – do they have any religious significance? And of course you’re also right on the spelling of waste vs waist, which has now been corrected.
Hi I been trying to get this tattoo for quite sometime but all I could come up with is this.
“This too will pass” وهذا أيضا سوف يمرّ
I’d like to know if that’s the correct spelling. Thank you so much in advance for all your help. God bless.
Hello my name is carmen.. nd ive been trying for years to get this translated… can u translate it for me plz.. i will greatly appreciate it nd thanks you so much..
ask and it will be given to you seek and you will find knock and it will be open to you matthew 7:7
Ask, and it shall be given you; seek, and ye shall find; knock, and it shall be opened unto you
Hi i just want to know the proper arabic spelling of the quote “only god shall judge me” .
Please and thank you
Tattoos are barely seen in the east!! Because of our religion and culture , I’m from jordan and I speak Arabic as my mother language and english as a second language , I can help translating for you 😉
hi i am looking for the symbol in arabic for heaven an i am unable to find it….
Hi Jennifer! There are six different designs for “Heaven” in my Arabic Tattoos ebook.
Hi Shatha I would appreciate it if you could please help me out I recently posted above this here : “ This too will pass ” وهذا أيضا سوف يمرّ
I would like to know if that is correct, I searched & found it on google.. Thank in advance. Courtney.
Can you translate Just Breathe In Arabic for me please? Also, can you translate my name in Arabic it’s Brandie. Thank you so much!
Can somebody helps me to translate faith??
hi tere can some one PLEASE translate this in arabic: that which does not kill me makes me stronger
thanks 🙂 x
there*
arabicgenie, this is jennifer what do the signs look like thanks
pls help jon marie,jean marie,john marino in arabic thnkx.
Hi can you help me for the strength or my strength in arabic words thank you
Hi Jessy. I have translated strength in Arabic here already.
السلام
هل هذه موضة جديده في الوشم ؟ و من اين جاءت؟
السلام عليك يا AIAA!
أعتقد أن هذه الظاهرة بدأت في السنوات الاخيرة والاسباب متعددة.
Hi, can you help me translate this word: “Ulacoraifal”
It’s means a lot to me, but i can’t find a unique way to wrote
Thank you
Hi, i would like to know if u cold spell “kupe” for me.its really important to me.thank you
Hello ArabicGenie! I was just wondering if you could translate “love yourself” in arabic. Thanks 🙂
hello holly the translation of “love yourself” is “أحب نفسك”
أحب نفسك
ahebba nafsak
Helloo Arabic Genie..
can u please help me to find the exact words in arabic script “Strength of will” and “Destiny”
Hello Arabic Genie, not sure if you still reading this comments, I would like to get: Beauty is imperfection in arabic, could you please confirm this: الجمال هو النقص
Thank you so much!
Elloca
My wifes name is Azeema, could you please write her name in Arabic for me. Thank You.
Tatoos are not allowed in islam so me being cant get a totoo done but if religion permitted. I would have. Gotten. My parents. Name on my forehand
Randy.. عزيمة = determination
Hello guys,i am an arab and i was checking your arabic tattoos and most of them are actually wrong, don’t follow google translation it always messes up. Arabic is kinda difficult, so you may wanna make sure everything is correct before getting yourself tattoed, anyways i would recommend that you would ask someone who’s excellent in arabic or a person whose first language is arabic.
Hi I need help with the translation “No fear” can someone help me with that?
Hi
Can you please translate the word “strive” ( eg: to stive to do ones best )
Hello,
Please translate “Strength of a warrior” and “Virtuous” in Syrian-Arabic writing.
Thank you